|
ДВОИЧНОЕ КОДИРОВАНИЕ
Двоичная
система была придумана задолго до появления
компьютеров. Ещё великий немецкий математик Готфрид
Вильгельм Лейбниц увидел в двоичной системе особый
скрытый смысл. Действительно, двоичная система
предельна проста:
используется всего две
цифры - 0 и
1;
таблица
умножения состоит всего из трёх строк:
0*0=0
0*1=0
1*1=1
К
недостаткам двоичной системы можно отнести только
"длину" записи чисел (чем меньше в системе цифр, тем
длиннее будет запись числа):
200210 = 111110100102
Однако, этот досадный факт не помешал инженерам
использовать двоичную систему при конструкции
электронных схем. Перевести число из двоичной
системы в привычную десятичную может не только
вычислительная машина, но и человек. Для удобства
запишем двоичное число в таблицу поразрядно,
пронумеруем разряды в следующей строке (справа
налево, начиная с 0) и выпишем соответствующие
степени двойки (справа налево с 0-й степени). Для
числа 111110100112
таблица выглядит так
|
число |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
|
n |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
0 |
2n |
1024 |
512 |
256 |
128 |
64 |
32 |
16 |
8 |
4 |
2 |
1 |
Единицы
в первой строке таблицы указывают, какие степени
двойки нужно сложить, чтобы получить число:
1024+512+256+128+64+16+2+1=2003
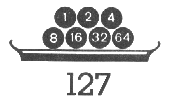 Двоичная система счета позволяет найти набор гирь, с
помощью которого можно получить любой вес от 1 г. до
127 г. Этот набор состоит из гирь в 1 г, 2 г, 4 г, 8
г, 16 г, 32 г и 64 г. Если надо, например, отвесить
57 г, то берем гири в 32 г, 16 г, 8 г и 1 г.
Подсчитайте, что вместе они составляют как раз 57.
Равенство
57=32+16+8+1 можно записать с помощью двоичной
системы счисления. В нашей записи 32=25.
А так как в двоичной системе вместо 2 пишут 10, то
32 записывается так: 105, то есть
100000. Точно так же 16=24=10000,
8=23=1000, и поэтому
57=100000+10000+1000+1=111001 (по двоичной системе).
А если
нужно взвешивать вещи побольше, то к нашему набору
гирь надо добавить разновески в 128 г, 265 г, 512 г
и далее удваивать полученные числа.
|
