|
Составные числа. Признаки делимости
Тренажер:
Угости пингвинов
соком
Для проверки
того, является данное число составным или нет,
требуется выполнить достаточно большое количество
делений его на меньшие числа. Для некоторых
делителей существуют признаки, позволяющие
устанавливать делимость на них без выполнения самого
деления значительно проще. Такие признаки называют
признаками делимости.
Пусть
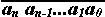 -
десятичная запись числа N, т. е. -
десятичная запись числа N, т. е.
N=an
*10+an-1*10n-1+...+a1*10+a0
,
0<aj<9
-
Признак делимости на
10. Число
N делится на 10 только в том случае, если
его младшая цифра
a0
равна 0.
-
Признак делимости на
5. Число N делится на 5
только в том случае, если его младшая цифра
a0
делится на 5, т. е. равна 0
или 5.
-
Признак делимости на
2. Число N делится на 2
только в том случае, если его младшая цифра
a0
делится на 2.
Каждый
из этих признаков следует из того, что разность N-a0
делится на 10, т. е. делится на числа 10, 5 и 2, а,
значит, числа N и
a0
одновременно делятся или не делятся на 10, 5 или 2.
Для
обоснования признака делимости на 4 заметим, что
разность
N-(2a1+a0)=(N-(10a1+a0))+((10a1+a0)-(2a1+a0)
делится на 4 (число (N-10a1+a0)
делится даже на 100, а оставшееся слагаемое равно
8a1.
Поэтому числа N и
2a1+a0т
одновременно делятся или не делятся на 4.
Проверим это, например, для
числа 1234:
1234-(1+2+3+4)=1224=9*136.
Можно
попытаться выполнить проверку указанного свойства и
на других числах. Для того, чтобы понять его
причину, попробуем вычисления с числом 1234
представить иначе:
1234-(1+2+3+4)=(1000-1)+(200-2)+(30-3)=(1000-1)+2(100-1)=999+2*99+3*9=
=9(111+2*11+3).
Как
видим, дело в том, что числа 10-1, 102-1,
103-1 делятся на 9. Эта делимость имеет
место и для любого числа вида 10k-1.
Действительно,
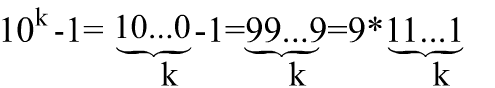
В общем случае разность
между числом N=-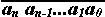 и сумма его цифр равна
и сумма его цифр равна
an*10+an-1*10n-1+...+an*10+an-(an+an-1+...+a1+a0)=an(10n-1-1)+...+a1(10-1).
Как мы только что
установили, все разности в скобках делятся на 9.
Поэтому делится на 9 и разность между числом N
и суммой его цифр. Иначе свойство делимости на 9
можно высказать так:
- натуральное число и
сумма его цифр имеют
одинаковые остатки при деление на 9.
Задача
Напишите какое-нибудь число.
Вычтите из него сумму цифр, стоящих на нечетных
местах, если считать справа налево. Затем прибавьте
сумму цифр, стоящих на четных местах. Результатом
всегда будет являться 11.
Например, если написано
число 239765, то сумма его цифр, стоящих на нечетных
местах, равна 5+7+3=15, а на четных местах 6+9+2=17.
Проделав указанные вычисления, найдем
239765-15+17=239767=11*21797.
Попробуйте объяснить это
свойство. На нем основан
признак делимости
на 11.
Вычислим сумму чисел данного числа, стоящих на
нечетных местах, если считать справа налево, а затем
вычислим сумму остальных чисел. Из большей суммы
вычтем меньшую. Данное число делится на 11 только в
том случае, если делится на 11 полученная разность.
|