В начало
 
Краткий обзор развития  понятия числа
 
Немного теории
 
Системы счисления
 
Шкатулка
 
О нас
 

Составные числа. НОД

  • Если a и b- целые неотрицательные числа, делящиеся на некоторое натуральное число d, то говорят, что d есть общий делитель a и b.
  • Единица есть общий делитель любых двух целых чисел. При a=b=0 любое натуральное число будет общим делителем a и b.
  • Если a>0, то каждый делитель числа a не превосходит a по величине, и, значит, среди общих делителей чисел a и b имеется самый большой. Этот самый большой из общих делителей чисел a и b называется их наибольшим общим делителем.
  • Для наибольшего общего делителя чисел a и b имеется специальное обозначение НОД(a, b).
  • Так, например, НОД(2, 4)=2. Числа 5 и 6 не имеют общих делителей, кроме 1, поэтому НОД(5, 6)=1.
  • Для любого натурального числа a имеем НОД(a, 1)=1 (ведь 1 не может делится ни на какое натуральное число, отличное от 1).
  • Для любого натурального числа a справедливо равенство НОД(a, 0)=a. Действительно, оба числа a и 0 делятся на a. Но никакое число, большее a не может быть делителем a.

    Очень полезно уметь находить НОД двух чисел. Например, это может пригодится, если мы захотим представить какое-нибудь рациональное число в виде дроби, имеющей по возможности меньший числитель и знаменатель. Например:

   6665      215*31      31

 11395      215*53      53

Алгоритмы нахождения НОД

Школьный

тренажер: Построй мост

Чтобы найти НОД двух чисел нужно:

  • Разложить оба числа на простые множители
  • Выделить общие множители
  • НОД равен произведению общих множителей

   Пример:

24=3*2*2*2         90=3*3*2*5

НОД (24, 90)=3*2=6

Алгоритм Евклида

Если и r- остаток от деления a и b, то

НОД (a, b)=НОД (b, r).

    Другими словами, наибольший общий делитель двух натуральных чисел равен наибольшему общему делителю меньшего из них и остатка от деления большего на меньшее. На этом основан Алгоритм Евклида

Пример:

Вычислим НОД(a, b())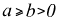

Вычислим НОД(11395, 6665)

  • Разделим a на b.

  • Разделим b на остаток от деления a на b.

  • Будем последовательно продолжать деление, пока не получим в остатке ноль.

  • Последний не нулевой остаток и есть НОД(a, b)

9091/1234=7(ост.453),
1234/453=2(ост.328),
453/328=(ост.125),
328/125=2(ост.78),
125/78=(ост.47),
78/47=(ост.31),
47/31=(ост.16),
31/16(ост.15),
16/15(ост.1),
15/15=0.

  • Бинарный

    • Бинарный алгоритм иногда более удобный, чем Алгоритм Евклида.

    • Если a и b оба четны, то НОД(a, b)=2(a/2, b/2);

    • Если a четно и b нечетно, то НОД(a, b)=(a/2, b);

    • Если a и b оба нечетны и , то НОД(a, b)=(a-b, b).

    Пример:

    НОД(1978, 2666)=2*(989, 1333)=2*(989, 344)=2*(989, 172)=2*(989, 86)=2*(989, 43)=2*(946, 43)=
    =2*(473, 43)=2*(430, 43)=2*(215, 43)=2*(172, 43)=2*(86, 43)=2*(43, 43)=2*43=86.

    НОД(1978. 2666)=86

        Иногда можно комбинировать Алгоритм Евклида и этот так называемый бинарный алгоритм;

    Задача:

    Докажите, что:

    • справедливо равенство НОД(a*b, a*c)=a*НОД(b, c) и, в частности, наибольший общий делитель двух чисел делится на любой их общий делитель;

    • если НОД(a, c)=1, то имеет место равенство НОД(a*b, c)=НОД(b, c)

     
     
    Hosted by uCoz