Составные числа. НОК
 

Наименьшее общее кратное двух чисел N и M есть, как известно, наименьшее из натуральных чисел, делящихся на N и M. Пусть N и M имеют вид

^,  

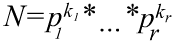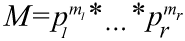
где показатели k и m неотрицательны, а натуральное число

^{,   , ...,  ,}

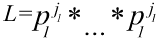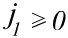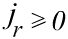делится на N и M. Тогда по доказанному в НОД справедливы неравенства

^{,   , ...,}  

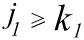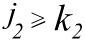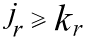
Общее кратное будет наименьшим, если каждый показатель j принимает наименьшее возможное значение, т. е. j₁ равен большему из чисел k₁ и m₂ и т. д. В соответствии с этим правилом находим:

НОК (3132, 7200)=2⁵*3³*5²*29=626400

Тренажер: Построй мост