Составные числа. Разложение на множители

Чтобы показать, что число является составным надо представить его в виде произведения хотя бы двух множителей, отличных от единицы. Не всегда эта задача решается легко.

В 1905 г. было доказано, что так называемое число Ферма с номером 7
F₇ = 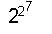+1=2¹²⁸+1 =340282366920938463374607431768211457
составное. Лишь в 1970 г. с использованием ЭВМ было найдено его разложение на множители:
F₇ =59649589127497217*5704689200685129054721,
причем оба множителя - простые числа.
Число F8 =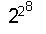+1=2²⁵⁶+1  тоже составное. Оно раскладывается на два простых множителя, больший из них записывается 62 цифрами в десятичной системе.
Число F₉= 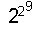   +1=2⁵¹²+1=2424833*А, где А - составное число. Но даже с помощью ЭВМ до сих пор не удаётся разложить А на множители.

Если число N может быть представлено в виде разности квадратов двух чисел, то разложение его на множители получается немедленно:

                           N=a²-b²=(a²-ab)+(ab+b²)=a(a-b)+b(a-b)=(a+b)(a-b)

Способ разложения чисел, основанный на этой идее, был предложен французским математиком П.Ферма(1601-1665)
    Будем последовательно строить числа вида a²-N  и проверять, являются они квадратами или нет. Как только разность a²-N станет равной квадрату целого числа b² , мы будем иметь равенство равенство N=a²-b² и, значит разложение числа N на множители.
 Так как   (a+1)²-a²=(a+1+a)(a+1-a)=2a+1 то следующее число  (a+1)²-N может быть построено из предыдущего a²-N добавлением числа 2a+1. Это упрощает вычисления.
                                        

ПРИМЕР:
N=2077, так как 45²<2077<46² , то начальное значение a равно 46

a²-N=46²-2077=39
2a+1=2*46+1=93

Таким образом (46+3)²-2077=18² и 2077=49²-18²=(49+18)(49-18)=63*31